Gradient Descent

Introduction

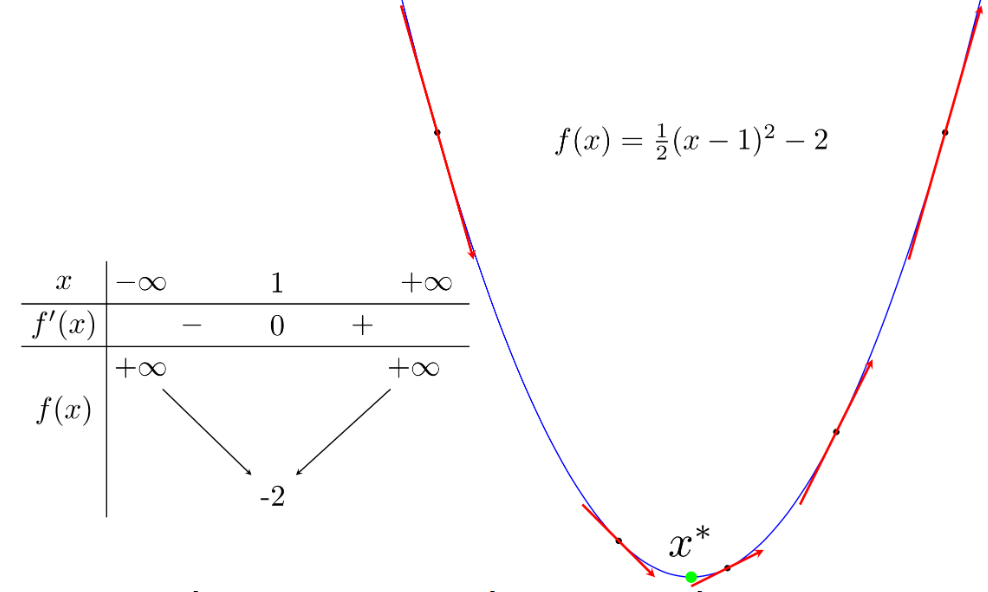
You might find the following image familiar:

The green point is a local minimum, which is also the point where the function reaches its smallest value. From now on, I will use local minimum to refer to the point of minimum, and global minimum to refer to the point where the function reaches its smallest value. A global minimum is a special case of a local minimum.

Assume we are interested in a single-variable function that is differentiable everywhere. Let me remind you of a few familiar facts:

1. A local minimum \(x^*\) of a function is a point where the derivative \(x^*\) is zero. Furthermore, in its vicinity, the derivative of points to the left of \(x^*\) is non-positive, and the derivative of points to the right of \(x^*\) is non-negative.

2. The tangent line to the graph of the function at any point has a slope equal to the derivative of the function at that point.

In the image above, points to the left of the green local minimum have negative derivatives, and points to the right have positive derivatives. For this function, the further left from the local minimum, the more negative the derivative, and the further right, the more positive the derivative.

In Machine Learning and Optimization, we often need to find the minimum (or sometimes the maximum) of a function. Generally, finding the global minimum of loss functions in Machine Learning is very complex, even impossible. Instead, people often try to find local minima and, to some extent, consider them the solution to the problem.

Local minima are solutions to the equation where the derivative is zero. If we can somehow find all (finite) local minima, we only need to substitute each local minimum into the function and find the point that makes the function smallest (this sounds familiar, doesn’t it?). However, in most cases, solving the equation where the derivative is zero is impossible. This can be due to the complexity of the derivative’s form, the high dimensionality of the data points, or the sheer number of data points.

The most common approach is to start from a point we consider close to the solution and then use an iterative process to gradually reach the desired point, i.e., until the derivative is close to zero. Gradient Descent (abbreviated as GD) and its variants are among the most widely used methods.

Since the knowledge about GD is quite extensive, I will divide it into two parts. Part 1 introduces the idea behind the GD algorithm and a few simple examples to help you get familiar with this algorithm and some new concepts. Part 2 will discuss improved GD methods and GD variants in problems with high dimensionality and large data points, known as large-scale problems.

Gradient Descent for Single Variable Functions

Returning to the initial image and some observations I mentioned. Suppose $x_{t}$ is the point found after the $t$-th iteration. We need an algorithm to bring $x_{t}$ as close to $x^*$ as possible.

In the first image, we have two more observations:

1. If the derivative of the function at $x_{t}$: $f’(x_{t}) > 0$, then $x_{t}$ is to the right of \(x^*\) (and vice versa). To make the next point \(x_{t+1}\) closer to \(x^*\), we need to move \(x_{t}\) to the left, i.e., in the negative direction. In other words, we need to move in the opposite direction of the derivative: $x_{t+1} = x_{t} + \Delta$ Where $\Delta$ is a quantity opposite in sign to the derivative $f’(x_{t})$.

2. The further $x_{t}$ is from $x^*$ to the right, the larger $f’(x_{t})$ is (and vice versa). Thus, the movement $\Delta$, in the most intuitive way, is proportional to $-f’(x_{t})$.

The two observations above give us a simple update rule: $x_{t+1} = x_{t} - \eta f’(x_{t})$

Where $\eta$ (read as eta) is a positive number called the learning rate. The minus sign indicates that we must go against the derivative (This is also why this method is called Gradient Descent - descent means going against). These simple observations, although not true for all problems, are the foundation for many optimization methods and Machine Learning algorithms.

Simple Example with Python

Consider the function $f(x) = x^2 + 5\sin(x)$ with the derivative $f’(x) = 2x + 5\cos(x)$ (one reason I chose this function is that it is not easy to find the solution of the derivative equal to zero like the function above). Suppose we start from a point $x_{0}$, at the $t$-th iteration, we update as follows: $x_{t+1} = x_{t} - \eta(2x_{t} + 5\cos(x_{t}))$

As usual, I declare a few familiar libraries:

# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
import math
import numpy as np 
import matplotlib.pyplot as plt

Next, I write the functions:

1. grad to calculate the derivative

2. cost to calculate the function’s value. This function is not used in the algorithm but is often used to check if the derivative is calculated correctly or to see if the function’s value decreases with each iteration.

3. myGD1 is the main part that implements the Gradient Descent algorithm mentioned above. The input to this function is the learning rate and the starting point. The algorithm stops when the derivative’s magnitude is small enough.

def grad(x):
    return 2*x+ 5*np.cos(x)

def cost(x):
    return x**2 + 5*np.sin(x)

def myGD1(eta, x0):
    x = [x0]
    for it in range(100):
        x_new = x[-1] - eta*grad(x[-1])
        if abs(grad(x_new)) < 1e-3:
            break
        x.append(x_new)
    return (x, it)

Different Starting Points

After having the necessary functions, I try to find solutions with different starting points $x_{0} = -5$ and $x_{0} = 5$.

(x1, it1) = myGD1(.1, -5)
(x2, it2) = myGD1(.1, 5)
print('Solution x1 = %f, cost = %f, obtained after %d iterations'%(x1[-1], cost(x1[-1]), it1))
print('Solution x2 = %f, cost = %f, obtained after %d iterations'%(x2[-1], cost(x2[-1]), it2))

Solution    x1 = -1.110667, 
            cost = -3.246394, 
            obtained after 11 iterations
Solution    x2 = -1.110341, 
            cost = -3.246394, 
            obtained after 29 iterations

Thus, with different initial points, our algorithm finds similar solutions, although with different convergence speeds. Below is an illustration of the GD algorithm for this problem (best viewed on Desktop in full-screen mode).

From the illustration above, we see that in the left image, corresponding to $x_{0} = -5$, the solution converges faster because the initial point $x_0$ is closer to the solution $x^* \approx -1$. Moreover, with $x_{0} = 5$ in the right image, the path of the solution contains an area with a relatively small derivative near the point with an abscissa of 2. This causes the algorithm to linger there for quite a while. Once it passes this point, everything goes smoothly.

Different Learning Rates

The convergence speed of GD depends not only on the initial point but also on the learning rate. Below is an example with the same initial point $x_{0} = -5$ but different learning rates:

We observe two things:

1. With a small learning rate $\eta = 0.01$, the convergence speed is very slow. In this example, I chose a maximum of 100 iterations, so the algorithm stops before reaching the destination, although it is very close. In practice, when calculations become complex, a too-low learning rate will significantly affect the algorithm’s speed, even preventing it from ever reaching the destination.

2. With a large learning rate $\eta = 0.5$, the algorithm quickly approaches the destination after a few iterations. However, the algorithm does not converge because the step size is too large, causing it to circle around the destination.

Note: Choosing the learning rate is crucial in real-world problems. The choice of this value depends heavily on each problem and requires some experimentation to select the best value. Additionally, depending on some problems, GD can work more effectively by choosing an appropriate learning rate or selecting different learning rates at each iteration. I will return to this issue in part 2.

Algorithm Steps

The steps in the Gradient Descent algorithm are as follows:

1. Initialize Parameters: Start with an initial guess for the parameters, denoted as $\theta$, that minimize the objective function $f(\theta)$. This could be any starting point, often chosen randomly.

2. Compute the Gradient: At the current parameter values, calculate the gradient (partial derivatives) of $f(\theta)$ with respect to $\theta$. The gradient vector points in the direction of the steepest increase.

3. Update Parameters: Update the parameters by moving in the opposite direction of the gradient by a factor of the learning rate $\alpha$: \(\theta = \theta - \alpha \nabla f(\theta)\) $\nabla f(\theta)$ is the gradient of the function at $\theta$ and $\alpha$ is a small positive number.

4. Iterate Until Convergence: Repeat steps 2 and 3 until the change in the function value $f(\theta)$ is smaller than a chosen threshold, or a maximum number of iterations is reached.

Key Parameters {#key-parameters .unnumbered}

• Learning Rate ($\alpha$): This controls the step size during the update. A small learning rate makes convergence slow but more stable, while a large learning rate might cause overshooting or divergence.

• Convergence Criteria: Gradient Descent iterates until the function’s value change is negligible (below a threshold) or until a fixed number of steps is completed.

Types of Gradient Descent

Gradient Descent has three main variants, depending on how often gradients are calculated:

1. Batch Gradient Descent: Calculates the gradient using the entire dataset. It is computationally expensive but offers a stable descent path.

2. Stochastic Gradient Descent: Calculates the gradient using one data point at a time. This is less stable but faster and can help in escaping local minima.

3. Mini-Batch Gradient Descent: A hybrid of Batch and Stochastic Gradient Descent, it calculates the gradient on small subsets (mini-batches) of data, balancing stability and computational efficiency.

Applications Beyond Machine Learning

Gradient Descent is widely used in:

• Physics: For optimizing physical models and simulations.

• Economics: To find optimal parameters in cost functions and utility functions.

• Engineering: For minimizing error in control systems or optimizing structural parameters.

Advantages and Disadvantages

Advantages:

• Simple and Versatile: Gradient Descent is straightforward to implement and applicable to a wide range of optimization problems.

• Efficient for Large Problems: Especially in mini-batch or stochastic variants, it can handle large datasets and complex functions.

Disadvantages:

• Sensitive to Learning Rate: Choosing an appropriate learning rate can be challenging.

• May Converge to Local Minima: Particularly in non-convex functions, it can get stuck in local minima (though variations like Stochastic Gradient Descent help mitigate this).