Extreme Gradient Boosting (XGBoost)

Classification and Regression Trees (CART)

XGBoost uses Classification and Regression Trees (CART) as base learners to build its model. Unlike traditional decision trees, which focus solely on boundaries for classification tasks, CART in XGBoost optimizes by minimizing a specified loss function, making it versatile for both classification and regression tasks. The CART algorithm, developed by Leo Breiman, Jerome Friedman, Richard Olshen, and Charles Stone in 1984, is a foundational machine learning model used for predictive tasks.

Overview of CART in XGBoost

CART is a form of decision tree algorithm that builds a tree structure to predict a target variable by recursively splitting data at nodes based on an optimal split. Each split is determined using criteria that maximize homogeneity within the resulting subsets. CART can handle both categorical target variables (Classification Trees) and continuous target variables (Regression Trees).

Structure and Function of CART

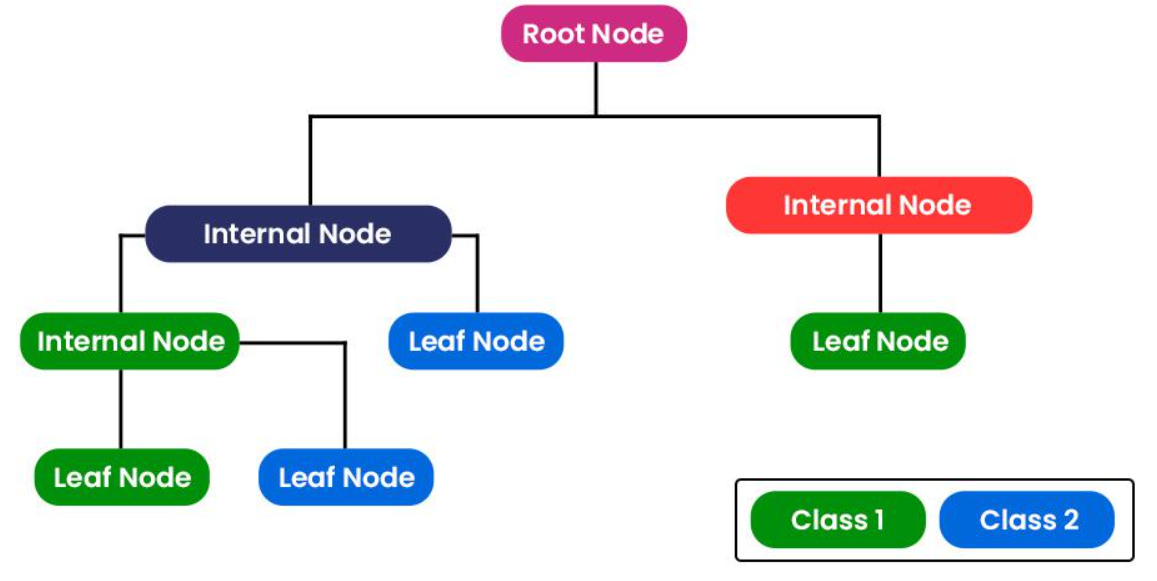
A CART model is structured as a binary tree with nodes representing decision points and branches corresponding to the possible outcomes of each decision. The key features include:

• Root Node: Represents the entire dataset, serving as the initial decision point.

• Internal Nodes: Represent split points based on predictor variables, dividing the data into subgroups.

• Leaf Nodes: Terminal nodes that contain the predicted outcome, either a class label (for classification) or a continuous value (for regression).

Types of Trees in CART

CART consists of two main types of trees:

• Classification Trees: Designed for categorical target variables, where the algorithm assigns a class label to each leaf node. These trees use criteria like Gini impurity to determine the best split, ensuring the purity of each subset.

• Regression Trees: Built for continuous target variables, where each leaf node represents a predicted value. The trees are split using criteria based on residuals, aiming to minimize the difference between the actual and predicted values.

Splitting Criteria in CART

CART uses a greedy algorithm to determine the optimal split at each node by maximizing homogeneity in the resulting subgroups. The splitting criteria differ based on the type of task:

• Classification (Gini Impurity): The Gini impurity measures the probability of misclassifying a randomly chosen element from a subset. It is computed as: \(\text{Gini} = 1 - \sum_{i=1}^n p_i^2\) where $p_i$ represents the probability of an instance being classified to a particular class. A lower Gini impurity indicates higher purity within the subset.

• Regression (Residual Reduction): For regression tasks, CART uses residual reduction, which aims to minimize the sum of squared errors within each subset. The goal is to achieve splits that result in subsets with minimal variance.

Algorithm and Steps for CART

The CART algorithm proceeds as follows:

1. Identify Best Split Point for Each Input: Each feature is evaluated to find the best split point that maximizes homogeneity in the subsets.

2. Select the Optimal Split: Based on the candidate splits, the algorithm selects the one that best reduces impurity or residuals, depending on the task.

3. Recursive Splitting: The chosen split divides the data, and the process is repeated for each subset until stopping criteria are met.

4. Stopping Criteria: The process halts when further splits do not significantly reduce impurity, or when the maximum tree depth is reached.

Pruning in CART

To avoid overfitting, CART often uses pruning techniques to simplify the tree. Two common approaches are:

• Cost Complexity Pruning: This involves calculating the cost of each node and removing nodes that provide minimal gain.

• Information Gain Pruning: Nodes are pruned based on the information gain they provide, with nodes having low information gain being removed.

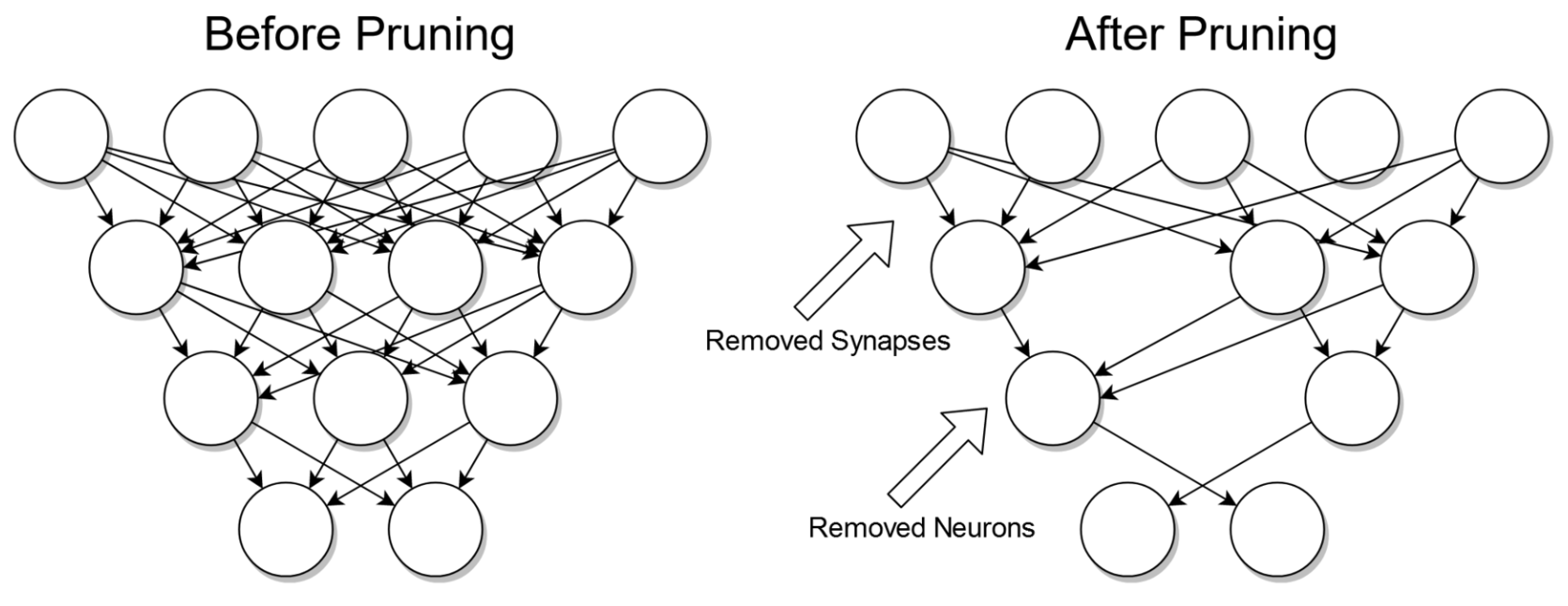
Description: This figure illustrates the concept of pruning in neural networks, which is a technique used to reduce the complexity of a network by removing unnecessary elements. The left side shows a fully connected network before pruning, while the right side shows the same network after pruning.

• Before Pruning: The network is fully connected, meaning each neuron in one layer is connected to every neuron in the next layer. This setup often leads to high computational and memory requirements due to the large number of connections (synapses) and neurons.

• After Pruning: Pruning removes certain neurons and synapses that are determined to be non-essential to the network’s performance. Removed synapses are depicted with arrows pointing to the empty connections, while removed neurons are shown with arrows pointing to the empty circles where nodes previously existed.

Gini Impurity in CART

The Gini impurity index, used in classification tasks, is a measure of the probability of misclassifying a randomly chosen element. Its formula is given by:

\[\text{Gini} = 1 - \sum_{i=1}^n (p_i)^2\]

where $p_i$ is the probability of an object being classified to a specific class. The closer the Gini index is to zero, the purer the subset.

Exact Greedy Algorithm

The Exact Greedy Algorithm in XGBoost exhaustively searches for the best possible split at each node of the tree by evaluating all potential split points across all features. It selects the split that maximizes the gain in the objective function, which is critical for optimal partitioning of the data.

The gain from a split can be defined mathematically as follows:

\[\text{Gain} = \frac{1}{2} \left( \frac{(\sum_{i \in L} g_i)^2}{\sum_{i \in L} h_i + \lambda} + \frac{(\sum_{i \in R} g_i)^2}{\sum_{i \in R} h_i + \lambda} - \frac{(\sum_{i} g_i)^2}{\sum_{i} h_i + \lambda} \right)\]

where: - $L$ and $R$ represent the left and right child nodes after a potential split. - $g_i$ is the gradient of the loss function with respect to the prediction for instance $i$. - $h_i$ is the Hessian, or the second derivative of the loss function. - $\lambda$ is a regularization term that helps prevent overfitting.

The use of both the gradient and Hessian allows for a more nuanced understanding of the loss landscape, enabling better decision-making for splits. However, this algorithm can be computationally intensive because it requires sorting the feature values and evaluating every possible split for all features.

Approximate Algorithm

To mitigate the computational burden of the exact greedy approach, XGBoost implements an Approximate Algorithm. This algorithm generates candidate splits based on the distribution of feature values and uses a method of aggregating gradient statistics to find the best split from these candidates.

The approximation process can be summarized as follows:

1. Propose Candidate Splits: The algorithm divides the feature values into buckets based on percentiles (e.g., 25th, 50th, 75th percentiles). This step reduces the number of possible splits significantly while still capturing the overall distribution of the data.

2. Aggregate Gradient Statistics: For each bucket, it calculates the accumulated gradient ($G_k$) and Hessian ($H_k$) statistics:

\[G_k = \sum_{j \in \{j|s_k,v \geq x_{jk} > s_k,v-1\}} g_j\] \[H_k = \sum_{j \in \{j|s_k,v \geq x_{jk} > s_k,v-1\}} h_j\]

3. Select the Best Split: Using the aggregated statistics, the algorithm evaluates splits based on the gain formula, akin to the exact greedy method, but only considers the candidates derived from the buckets:

\[\text{Gain}_{\text{approx}} = \frac{1}{2} \left( \frac{(G_L)^2}{H_L + \lambda} + \frac{(G_R)^2}{H_R + \lambda} - \frac{(G)^2}{H + \lambda} \right)\]

This method significantly decreases computational complexity and is particularly effective in distributed and out-of-core settings, allowing XGBoost to handle large datasets efficiently.

Construction of Candidate Splits

The split finding algorithm in XGBoost is designed to efficiently propose candidate splits by using methods that reduce computational overhead while maintaining statistical accuracy. This approach allows XGBoost to perform well on large datasets, making it a popular choice for machine learning practitioners.

One key technique is the use of weighted quantile sketching, which enables XGBoost to select candidate split points that are statistically representative of the data distribution, rather than exhaustively evaluating all possible splits. By focusing on statistically significant splits, the algorithm achieves a balance between performance and computational efficiency.

Weighted Quantile Sketch

The weighted quantile sketch technique in XGBoost is a method for constructing candidate split points by approximating the distribution of weighted data, which is especially useful for large datasets. This approach ensures that the candidate splits reflect the distribution of the data accurately while reducing computational overhead.

• Definition: Weighted quantile sketch is a data structure that approximates quantiles in a dataset where each data point has an associated weight. Unlike standard quantile methods, which assume all instances are equally important, weighted quantile sketch accounts for weights in the dataset, enabling more accurate representation of data distribution in scenarios where instances carry different levels of importance (weights).

• Rank Function and Candidate Splits: Let \(\mathcal{D}_k = \{(x_{1k}, h_1), (x_{2k}, h_2), \dots, (x_{nk}, h_n)\}\) be the set of feature values $x_k$ along with their respective Hessian weights $h_i$ for each training instance $i$. We define the rank function $r_k(z)$ for a feature value $z$ as:

  \[r_k(z) = \frac{1}{\sum_{(x,h) \in \mathcal{D}_k} h} \sum_{\substack{(x, h) \in \mathcal{D}_k \\ x < z}} h,\]

  where $r_k(z)$ represents the cumulative proportion of instances whose feature value $x$ for feature $k$ is smaller than $z$. The objective is to find a set of candidate split points ${s_{k1}, s_{k2}, \dots, s_{kl}}$ such that:

  \[|r_k(s_{k,j}) - r_k(s_{k,j+1})| < \epsilon,\]

  where $\epsilon$ is an approximation factor that controls the precision of the split points. This rank-based selection ensures that split candidates are spaced proportionally, reflecting the weighted distribution of the data.

• Approximation Factor and Candidate Points: The approximation factor $\epsilon$ dictates the granularity of the candidate points, resulting in roughly $1/\epsilon$ candidate points. Each candidate point is weighted by its Hessian value $h_i$, representing the significance of the instance within the dataset. This weighted approach allows XGBoost to prioritize split points that better reflect data density and importance.

• Objective Reformulation: To incorporate weights effectively, the objective function is reformulated to focus on weighted squared loss. The objective can be approximated as:

  \[\sum_{i=1}^n \frac{1}{2} h_i (f_t(x_i) - g_i / h_i)^2 + \Omega(f_t) + \text{constant},\]

  where $g_i$ is the gradient and $h_i$ is the Hessian for each instance. This formulation is particularly advantageous for large datasets, as it enables efficient approximation without evaluating each split exhaustively.

• Distributed and Weighted Setting: Traditional quantile sketches work well for unweighted data but do not extend naturally to weighted datasets. For datasets with varying weights, naive quantile methods or sampling techniques do not guarantee theoretical accuracy. The weighted quantile sketch in XGBoost addresses this limitation by providing a method that supports merge and prune operations with provable accuracy. This allows for distributed computation with a guaranteed approximation error, making it ideal for large, distributed datasets.

• Use Case and Advantages: Weighted quantile sketching is particularly effective in distributed environments, where data may be partitioned across multiple machines. By creating a sketch structure that maintains a consistent approximation, the technique provides an efficient method to compute split candidates without sorting the full dataset. This is especially beneficial for large datasets where sorting or exhaustive search would be computationally prohibitive.

In summary, the weighted quantile sketch in XGBoost efficiently approximates quantiles in large, weighted datasets, enabling the model to propose accurate split candidates even in distributed computing environments. This technique is essential for XGBoost’s scalability and efficiency, allowing it to handle datasets with weighted instances while maintaining computational speed and accuracy.

Histogram-based Split Finding

The histogram-based split finding algorithm in XGBoost discretizes continuous features into a fixed number of bins, rather than evaluating splits on each unique feature value. This method reduces memory usage and speeds up computation by accumulating gradient and Hessian statistics for each bin instead of individual feature values.

• Definition: In the histogram-based method, continuous features are discretized by dividing the feature range into bins. Each bin represents a range of feature values, and gradient statistics are aggregated for all values within each bin.

• Formula: The binning process can be defined as:

  \[\text{Histogram Bin} = \left[ \min(x_i), \max(x_i) \right] \rightarrow B\]

  where $B$ denotes the bins created from continuous feature values $x_i$. For a feature $x$, if we divide its range into $K$ bins, each bin $b_k$ for $k = 1, 2, \dots, K$ can accumulate gradients $G$ and Hessians $H$ as:

  \[G_{b_k} = \sum_{i \in b_k} g_i, \quad H_{b_k} = \sum_{i \in b_k} h_i\]

  where $g_i$ and $h_i$ are the gradient and Hessian values for each instance $i$ in bin $b_k$.

• Use Case: Histogram-based split finding is ideal for large datasets, as it allows XGBoost to compute splits more efficiently without examining every feature value. This method is especially beneficial in high-dimensional data and when working with sparse data matrices, where many feature values may be zero.

Split Gain Calculation

To determine the quality of each candidate split, XGBoost calculates the split gain, which represents the reduction in the objective function after performing a split. The split gain formula is as follows:

\[\text{Gain} = \frac{1}{2} \left( \frac{\left( \sum_{i \in L} g_i \right)^2}{\sum_{i \in L} h_i + \lambda} + \frac{\left( \sum_{i \in R} g_i \right)^2}{\sum_{i \in R} h_i + \lambda} - \frac{\left( \sum_{i \in L \cup R} g_i \right)^2}{\sum_{i \in L \cup R} h_i + \lambda} \right) - \gamma\]

where:

• $L$ and $R$ represent the left and right child nodes after the split.

• $g_i$ and $h_i$ are the gradient and Hessian values for each instance $i$.

• $\lambda$ is the regularization parameter to penalize complex trees.

• $\gamma$ is the minimum loss reduction required to make a further split, controlling the complexity of the tree.

The split gain is used to select the best split point by maximizing the gain, thus ensuring that each split contributes to reducing the overall error of the model.

Advantages and Applications

The split finding algorithm in XGBoost, combining histogram-based binning with weighted quantile sketching, is advantageous in multiple scenarios:

• It reduces the computational cost of split finding, making XGBoost highly scalable for large datasets.

• It adapts well to high-dimensional data by focusing on significant splits rather than exhaustive search.

• Weighted quantile sketching enhances performance in distributed settings by approximating split points across partitions.

• Histogram-based binning is especially useful for dense data, allowing efficient gradient and Hessian accumulation within bins.

In summary, XGBoost’s split finding algorithm is designed to balance computational efficiency and statistical accuracy, making it highly effective for a wide range of machine learning tasks, particularly those involving large-scale or high-dimensional data.

Objective Function

The objective function in XGBoost consists of a differentiable convex loss function that measures the difference between predicted and actual values and a regularization term to penalize model complexity, which helps prevent overfitting.

Loss Function

The loss function quantifies the error between the predicted values and the actual target values. It varies based on the problem type.

For Regression For regression tasks, the squared error loss function is commonly used:

\[l(y_i, \hat{y}_i) = (y_i - \hat{y}_i)^2\]

where $y_i$ is the actual value, and $\hat{y}_i$ is the predicted value.

For Classification For binary classification, the logistic loss function is utilized:

\[l(y_i, \hat{y}_i) = -[y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]\]

where $y_i$ is the label (0 or 1), and $\hat{y}_i$ is the predicted probability.

Unregularized XGBoost Algorithm

Initialization

• Input: Training set ${(x_i, y_i)}_{i=1}^N$, a differentiable loss function $L(y, F(x))$, a number of weak learners $M$, and a learning rate $\alpha$.

• Initialize model with a constant value:

  \[\hat{f}_{(0)}(x) = \arg \min_{\theta} \sum_{i=1}^N L(y_i, \theta).\]

Iterative Process

• For each iteration $m = 1$ to $M$:

  • Compute the gradients for each instance:

    \[\hat{g}_m(x_i) = \left[ \frac{\partial L(y_i, f(x_i))}{\partial f(x_i)} \right]_{f(x)=f_{(m-1)}(x)}.\]

  • Compute the hessians for each instance:

    \[\hat{h}_m(x_i) = \left[ \frac{\partial^2 L(y_i, f(x_i))}{\partial f(x_i)^2} \right]_{f(x)=f_{(m-1)}(x)}.\]

  • Fit a base learner (e.g., tree) using the training set $\left{ x_i, \frac{\hat{g}m(x_i)}{\hat{h}_m(x_i)} \right}{i=1}^N$ by solving the optimization problem:

    \[\hat{\phi}_m = \arg \min_{\phi \in \Phi} \sum_{i=1}^N \frac{1}{2} \hat{h}_m(x_i) \left[ \phi(x_i) - \frac{\hat{g}_m(x_i)}{\hat{h}_m(x_i)} \right]^2.\]

  • Update the base learner:

    \[f_m(x) = \alpha \hat{\phi}_m(x).\]

  • Update the model:

    \[f_{(m)}(x) = f_{(m-1)}(x) - f_m(x).\]

Output

• The final model:

  \[f_{(M)}(x) = \sum_{m=0}^M f_m(x).\]

Regularization Term

Regularization in XGBoost penalizes complex models by adding a term:

\[\Omega(f) = \gamma T + \frac{1}{2} \lambda \sum_{j} w_j^2\]

where $T$ is the number of leaves in the tree, $w_j$ represents the leaf weights, $\gamma$ is the penalty for adding a new leaf, and $\lambda$ is the L2 regularization term on leaf weights. This regularization helps control the model’s complexity and enhances its generalization capabilities.

Sparsity-Aware Splitting Algorithm

The sparsity-aware splitting algorithm in XGBoost is designed to efficiently handle missing values and sparse data during split finding. Instead of imputing missing values or processing zero values as regular entries, XGBoost introduces default directions based on the gain from different split scenarios, allowing it to handle sparse datasets without unnecessary computations.

Objective of Sparsity-Aware Splitting

In many real-world datasets, certain features may have missing or zero values. The sparsity-aware splitting algorithm in XGBoost accommodates these by:

• Calculating split gains by considering missing values as going in either left or right directions.

• Choosing the split direction for missing values that maximizes the gain, leading to a more efficient and accurate model.

The algorithm works by sorting instances based on feature values, then iteratively computing gains for each split, considering both scenarios where missing values go to the left or the right child node.

Here’s the content formatted as correct pseudocode in markdown:

Pseudocode of Sparsity-Aware Splitting

Initialization

• Input:
  • $I$, instance set of the current node
  • $I_k = {i \in I \mid x_{ik} \neq \text{missing}}$, set of non-missing entries for feature $k$
  • $d$, feature dimension
• Compute initial sums:
  • $G \leftarrow \sum_{i \in I} g_i$
  • $H \leftarrow \sum_{i \in I} h_i$
  • $\text{gain} \leftarrow 0$

Iterative Process

1. Initialize:
   • $G_L \leftarrow 0$
   • $H_L \leftarrow 0$
2. Consider missing values going to the right:
   • For each $j \in I_k$:
     • $G_L \leftarrow G_L + g_j$
     • $H_L \leftarrow H_L + h_j$
     • $G_R \leftarrow G - G_L$
     • $H_R \leftarrow H - H_L$
     • $\text{score} \leftarrow \max(\text{score}, \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{G^2}{H + \lambda})$
3. Consider missing values going to the left:
   • Initialize:
     • $G_R \leftarrow 0$
     • $H_R \leftarrow 0$
   • For each $j \in I_k$:
     • $G_R \leftarrow G_R + g_j$
     • $H_R \leftarrow H_R + h_j$
     • $G_L \leftarrow G - G_R$
     • $H_L \leftarrow H - H_R$
     • $\text{score} \leftarrow \max(\text{score}, \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{G^2}{H + \lambda})$

Output

• Split and default directions with max gain.

Explanation of the Pseudocode

• Inputs:

  • $I$: The set of instances in the current node.

  • $I_k$: Subset of $I$ where feature $x_k$ is not missing for each instance.

  • $d$: The feature dimension under consideration for the split.

• Initialization:

  • Compute the overall gradient sum $G = \sum_{i \in I} g_i$ and Hessian sum $H = \sum_{i \in I} h_i$ for all instances in the node. These represent the total gradients and Hessians, which are used to calculate the overall gain.

• Loop over each feature $k$: The algorithm iterates over each feature to find the best split.

• Handling Missing Values Going Right:

  • For each possible split point $j$ (sorted in ascending order of feature values), accumulate the left and right gradients ($G_L$, $G_R$) and Hessians ($H_L$, $H_R$).

  • Calculate the gain score for this split as: \(\text{score} = \max\left(\text{score}, \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{G^2}{H + \lambda}\right),\) which measures the quality of the split.

• Handling Missing Values Going Left:

  • Repeat the above process but assume missing values go to the left. The instances are processed in descending order of feature values.

  • Update the gain score for each split point as in the previous step.

• Output: After processing all features, the algorithm outputs the split and default direction for missing values that yield the maximum gain.

Purpose and Advantages

The sparsity-aware splitting algorithm in XGBoost allows efficient handling of missing data during training. Instead of filling in missing values, the algorithm chooses the optimal direction (left or right) for missing entries based on the split gain, resulting in better performance and computational efficiency. This is especially useful for datasets with numerous missing values or sparse matrices, where zero values represent an absence of information rather than a meaningful feature value.

Second-order Approximation

XGBoost leverages a second-order Taylor expansion of the objective function, a key innovation that allows it to achieve faster convergence and precise updates. This approximation incorporates both the gradient and the Hessian (second derivative) of the loss function, which provides a more accurate representation of the loss behavior around the current estimate.

Taylor Expansion

The Taylor series expansion is used to approximate a function around a given point. For a function $f(x)$, the Taylor series expansion around a point $x_0$ up to the second-order term is:

\[f(x) \approx f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2} f''(x_0)(x - x_0)^2\]

where $f’(x_0)$ is the first derivative (gradient) and $f’‘(x_0)$ is the second derivative (Hessian) evaluated at $x_0$. This expansion uses both the slope and curvature of $f(x)$ around $x_0$ to approximate the function more accurately than using only the gradient.

Regularized Learning Objective

XGBoost optimizes a regularized objective function at each iteration, defined as:

\[\mathcal{L}(\phi) = \sum_{i=1}^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)\]

where:

• $l(y_i, \hat{y}_i)$ is the differentiable convex loss function that measures the error between the target $y_i$ and the prediction $\hat{y}_i$.

• $\Omega(f_k) = \gamma T + \frac{1}{2} \lambda |w|^2$ is the regularization term that penalizes the complexity of the model. Here, $T$ represents the number of leaves, $w$ is the vector of leaf weights, $\gamma$ controls the number of leaves, and $\lambda$ controls the $L2$-norm of leaf weights.

The regularization term $\Omega(f_k)$ helps smooth the learned weights to avoid overfitting.

Second-order Approximation (Taylor Expansion)

The second-order Taylor expansion allows for an efficient approximation of the objective function at each iteration. Given predictions $\hat{y}_i^{(t-1)}$ at the previous step $t-1$, the new objective function when adding function $f_t$ is approximated as:

\[\mathcal{L}^{(t)} \approx \sum_{i=1}^n \left[ l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2 \right] + \Omega(f_t)\]

where:

• $g_i = \frac{\partial l(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)}}$ is the gradient (first derivative) of the loss function with respect to the prediction.

• $h_i = \frac{\partial^2 l(y_i, \hat{y}_i^{(t-1)})}{\partial \hat{y}_i^{(t-1)^2}}$ is the Hessian (second derivative) of the loss function with respect to the prediction.

This expansion allows XGBoost to consider both the direction (through $g_i$) and the confidence (through $h_i$) of the update, which provides a more precise adjustment compared to using only first-order gradients.

Gain from a Split

To decide the best split at each node, XGBoost calculates the gain of the split, which represents the reduction in the objective function. For a dataset split into left $L$ and right $R$ subsets, the gain $\text{Gain}$ is defined as:

\[\text{Gain} = \frac{1}{2} \left( \frac{\left( \sum_{i \in L} g_i \right)^2}{\sum_{i \in L} h_i + \lambda} + \frac{\left( \sum_{i \in R} g_i \right)^2}{\sum_{i \in R} h_i + \lambda} - \frac{\left( \sum_{i \in L \cup R} g_i \right)^2}{\sum_{i \in L \cup R} h_i + \lambda} \right) - \gamma\]

where:

• $g_i$ and $h_i$ are the gradient and Hessian of the loss function for each data point $i$.

• $\lambda$ is a regularization parameter that penalizes leaf weights, reducing model complexity.

• $\gamma$ is the minimum loss reduction required to make a split. This helps control the depth of the tree and prevent overfitting.

This gain formula helps XGBoost choose splits that provide the maximum reduction in the objective function, thus enhancing the model’s accuracy iteratively.

Advantages of the Second-order Approximation in XGBoost

By incorporating the second-order term in the Taylor expansion, XGBoost can make more refined updates to the model parameters, which contributes to:

• Faster Convergence: More accurate updates allow the model to reach optimal solutions in fewer iterations.

• Improved Stability: The inclusion of the Hessian helps stabilize the updates, reducing the chances of oscillations.

• Enhanced Performance: With a more precise approximation, XGBoost can achieve higher accuracy with fewer boosting rounds.

Hyperparameters

XGBoost provides several hyperparameters that control various aspects of model behavior, such as learning rate, tree depth, and regularization terms. Proper tuning of these hyperparameters is essential for optimal model performance.

• Learning Rate (eta):

  • Definition: The learning rate, denoted as $\eta$, controls the contribution of each tree to the model. A lower learning rate slows down the learning process, often requiring more trees but resulting in better generalization.

  • Typical Range: Values between 0.01 and 0.3 are commonly used.

  • Effect: Lower values reduce the risk of overfitting but require more boosting rounds (trees).

• Tree Depth (max_depth):

  • Definition: The maximum depth of each tree controls its complexity. Shallow trees prevent overfitting but may underfit, while deeper trees capture more complex patterns at the risk of overfitting.

  • Typical Range: Values between 3 and 10 are generally effective, with 6 as a typical starting point.

  • Effect: Shallow trees (lower max_depth) reduce overfitting, while deeper trees allow for more complex interactions at the risk of overfitting.

• Minimum Child Weight (min_child_weight):

  • Definition: Controls the minimum sum of instance weights (Hessian) required in a child node to make a split. Higher values limit small nodes, reducing overfitting.

  • Typical Range: Values between 1 and 10.

  • Effect: Higher values restrict splits based on fewer data points, thus reducing overfitting.

• Gamma (min_split_loss):

  • Definition: Gamma specifies the minimum reduction in loss function needed to make a split. It controls tree complexity by setting a threshold for splits.

  • Typical Range: Values between 0 and 5.

  • Effect: Higher gamma values lead to fewer splits, reducing overfitting by simplifying the model.

• Subsample:

  • Definition: Specifies the fraction of training data to sample for each tree. Lower values introduce randomness, preventing overfitting by training each tree on only a portion of the data.

  • Typical Range: Values between 0.5 and 1.

  • Effect: Lower values help avoid overfitting by reducing model variance but may cause underfitting if set too low.

• Column Sampling (colsample_bytree, colsample_bylevel, colsample_bynode):

  • Definition:

    • colsample_bytree: Fraction of features sampled for each tree.

    • colsample_bylevel: Fraction of features sampled for each level of the tree.

    • colsample_bynode: Fraction of features sampled for each node.

  • Typical Range: Values between 0.5 and 1.

  • Effect: Using a subset of features at each split reduces correlation among trees, enhancing generalization and reducing overfitting.

• Lambda (L2 Regularization):

  • Definition: The L2 regularization term on leaf weights controls the complexity of the model. It penalizes large weights, reducing overfitting.

  • Typical Range: Values between 0 and 10.

  • Effect: Higher values make the model more conservative, dampening the impact of individual features.

• Alpha (L1 Regularization):

  • Definition: The L1 regularization term on leaf weights encourages sparsity, effectively setting less important weights to zero and improving feature selection.

  • Typical Range: Values between 0 and 10.

  • Effect: Higher values lead to simpler models, with more weights driven to zero, which can prevent overfitting.

• Scale_pos_weight:

  • Definition: Scales the gradient for positive instances, useful for imbalanced datasets.

  • Typical Range: Usually set to $\text{num_negative} / \text{num_positive}$.

  • Effect: Focuses the model on the minority class in imbalanced classification tasks, helping balance prediction accuracy.

• Number of Boosting Rounds (n_estimators):

  • Definition: Specifies the total number of trees to add to the model sequentially.

  • Typical Range: Varies significantly based on dataset and learning rate.

  • Effect: More trees generally improve accuracy but can increase overfitting risk. Early stopping can be used to determine the optimal number of rounds.

• Early Stopping:

  • Definition: Stops training when the validation set does not show improvement for a specified number of rounds, preventing overfitting and saving computational resources.

  • Typical Range: 10 to 50 rounds are commonly used.

  • Effect: Early stopping helps to prevent overfitting by stopping the training when no improvement is observed.

Hyperparameter Tuning Strategy: A good strategy for tuning these hyperparameters is:

1. Start with tuning max_depth and min_child_weight.

2. Adjust gamma to control model complexity.

3. Fine-tune subsample and colsample_bytree for further regularization.

4. Finally, adjust the learning rate and n_estimators for optimal performance.

Column Sampling

Column sampling is a technique in XGBoost where a random subset of features is selected at each split or tree construction step. This method helps prevent overfitting and improves the model’s ability to generalize by reducing the variance of the learned model.

Definition

Column sampling, also known as feature subsampling, refers to the process of randomly selecting a subset of features (columns) from the entire feature set. This subset is used to construct each tree or each split within a tree. In XGBoost, users can specify the fraction of features to sample using parameters such as:

• colsample_bytree: Fraction of features to consider for each tree.

• colsample_bylevel: Fraction of features to consider at each level of the tree.

• colsample_bynode: Fraction of features to consider at each node split.

This randomness in feature selection means that each tree in the ensemble may learn slightly different patterns, enhancing the model’s diversity.

Use Case

Column sampling is particularly useful in high-dimensional datasets where the number of features is large, and many of them may be irrelevant or redundant. By sampling a subset of features at each split, XGBoost can:

• Reduce the chance of overfitting on irrelevant features.

• Encourage each tree to capture different aspects of the data, leading to a more robust ensemble.

• Speed up training, as fewer features are considered at each split.

In scenarios like text classification or gene expression data, where feature dimensions can be very high, column sampling is advantageous as it avoids the risk of over-relying on a small set of features and can handle feature interactions more flexibly.

Purpose

The main purposes of column sampling in XGBoost are:

• Reduce Overfitting: By using only a fraction of features, the model does not overly depend on any single feature. This randomness forces the trees to learn unique patterns, reducing the model’s tendency to memorize noise in the training data.

• Improve Generalization: The randomness introduced by column sampling helps reduce variance. Since each tree only sees a subset of features, it becomes less likely for the ensemble model to be biased towards specific features, enhancing the generalization capabilities of the model on unseen data.

• Increase Computational Efficiency: When only a subset of features is considered at each split, the computational burden of searching for the best split across all features is reduced, leading to faster training times, especially with high-dimensional data.

Column sampling in XGBoost is inspired by techniques used in Random Forests, where feature subsampling at each split is a key factor contributing to the ensemble’s ability to avoid overfitting. The balance between selecting relevant features and introducing randomness is crucial for achieving a model that is both accurate and generalizable.

Parallelization

XGBoost incorporates parallelization techniques to speed up training on large datasets by taking advantage of multiple cores or distributed systems. Parallelization is crucial in XGBoost because it helps to reduce the time required for calculating gradients, finding optimal split points, and constructing trees.

Building Trees Level-wise

In XGBoost, trees are built level-wise rather than leaf-wise, which means all nodes at a given depth are split before moving to the next level. This structure allows for parallel computations, as the potential splits for all nodes at a given depth can be computed simultaneously. By doing so, XGBoost can:

• Reduce computation time, as each level is constructed concurrently.

• Improve memory usage efficiency by processing all nodes at a particular level before moving down the tree.

• Enhance model interpretability by ensuring balanced trees, as opposed to building very deep nodes one at a time.

This level-wise approach is particularly beneficial for handling wide datasets with many features, where each feature’s split can be evaluated independently at each level.

Parallel Computations

XGBoost performs parallel computation primarily by splitting the gradient and Hessian calculations among multiple processing threads. The main areas where parallelization is applied are:

• Gradient and Hessian Computations: XGBoost calculates the gradient and Hessian values for each instance in the dataset, which are used to find the optimal splits. These computations are distributed across multiple threads, significantly speeding up the calculation of gradients and Hessians.

• Split Finding: For each feature, potential split points are evaluated in parallel to determine the one that maximizes the gain in the objective function. This includes calculating sums of gradients and Hessians for left and right nodes for each potential split point, which can be independently processed for different features.

• Column Block Splitting: XGBoost divides features into blocks so that they can be processed concurrently. This columnar approach ensures that each thread focuses on a subset of features, further accelerating the split-finding process.

By distributing these computations across multiple threads or machines, XGBoost can significantly reduce training time, especially for large datasets. This parallelization strategy is flexible and adapts to both multi-core processors and distributed computing environments.

Scalability

XGBoost is designed to handle very large datasets efficiently, making it suitable for applications in big data and large-scale machine learning tasks. Scalability in XGBoost is achieved through techniques that allow it to operate effectively when datasets are too large to fit into memory or when distributed computing resources are available.

Out-of-core Computing

Out-of-core computing enables XGBoost to process datasets that exceed the system’s available memory by utilizing disk storage. This is achieved by:

• Data Sharding: Large datasets are split into smaller chunks, or shards, which are processed one at a time. Each shard fits into memory, while the rest are stored on disk.

• Pre-fetching: As one data shard is processed, the next shard is loaded from disk into memory, minimizing the I/O wait time. This pre-fetching approach helps maintain computational efficiency by overlapping I/O operations with processing.

• Incremental Updates: As each shard is processed, the model parameters are updated incrementally, allowing XGBoost to effectively learn from large datasets without requiring the entire dataset to be loaded into memory at once.

Out-of-core computing is particularly useful for scenarios where memory resources are limited, such as on commodity hardware, while maintaining high performance on large datasets.

Distributed Computing

XGBoost supports distributed computing, allowing the model to be trained across multiple machines in a cluster, which makes it highly scalable for large datasets. Distributed computing in XGBoost involves:

• Data Partitioning: The dataset is divided across multiple machines, with each machine handling a subset of the data. This reduces the memory and computational load on each individual machine.

• Synchronous Gradient Updates: Each machine calculates gradient and Hessian values for its data subset. These values are then synchronized across machines to ensure consistent updates of the model parameters.

• Parameter Averaging and Aggregation: After each iteration, the gradient and Hessian statistics are aggregated across all machines to compute the optimal split points. The model parameters are then updated in a synchronized manner across the cluster.

• Fault Tolerance: XGBoost can recover from failures in distributed settings, which enhances reliability in large-scale applications.

This distributed approach allows XGBoost to scale horizontally by adding more machines to the cluster, making it suitable for big data applications. It leverages frameworks like Apache Spark, Hadoop, and Dask for seamless integration in distributed environments, enabling it to handle billions of examples efficiently.