By

Convex Sets

Definition

The concept of convex sets might not be unfamiliar to you, as we have heard about convex polygons. "Convex" can be understood simply as "bulging outward" or "protruding outward." In mathematics, even a flat surface is considered convex.

Definition 1: A set is called a convex set if the line segment connecting any two points within the set lies entirely within the set.

Here are some examples of convex sets:

Examples of convex sets.

The black-bordered figures indicate that the boundaries are included, while the white-bordered figures indicate that the boundaries are not part of the set. A line or line segment is also a convex set according to the above definition.

Some real-world examples:

  • Suppose there is a convex-shaped room, and if we place a sufficiently bright light bulb at any position in the room, every point in the room will be illuminated.

  • If a country has a convex-shaped map, the flight path (Manhattan path) between any two cities within that country will lie entirely within its airspace. The map of Vietnam is not convex-shaped, as Cambodia is on the flight path between Hanoi and HCMC.

Below are some examples of nonconvex sets, which are not convex:

Examples of nonconvex sets.

The first three shapes are not convex because the dashed lines contain points that are not part of the set. The fourth shape, a square without a base, is not convex because the line connecting two points at the base may include points that are not part of the set. A curve is also not a convex set, as the line connecting two points is not entirely contained within the curve.

To describe a convex set mathematically, we use:

Definition 2: A set $\mathcal{C}$ is called convex if for any two points \(\mathbf{x}_1, \mathbf{x}_2 \in \mathcal{C}\), the point \(\mathbf{x}_{\theta} = \theta \mathbf{x}_1 + (1 - \theta) \mathbf{x}_2\) also lies in $\mathcal{C}$ for any $0 \leq \theta \leq 1$.

It is clear that the set of points in the form $\theta \mathbf{x}_1 + (1 - \theta) \mathbf{x}_2$ is the line segment connecting $\mathbf{x}_1$ and $\mathbf{x}_2$.

With this definition, the entire space is a convex set because any line segment lies within the space. The empty set can also be considered a special case of a convex set.

Examples

Hyperplanes and halfspaces

A hyperplane in $n$-dimensional space is the set of points that satisfy the equation:

\[a_1 x_1 + a_2 x_2 + \dots + a_n x_n = \mathbf{a}^T \mathbf{x} = b\]

where $b$ and $a_i$, $i = 1, 2, \dots, n$ are real numbers.

Hyperplanes are convex sets. This can be easily deduced from Definition 1. With Definition 2, we can also see this. If \(\mathbf{a}^T \mathbf{x}_1 = \mathbf{a}^T \mathbf{x}_2 = b\), then for any $0 \leq \theta \leq 1$:

\[\mathbf{a}^T \mathbf{x}_{\theta} = \mathbf{a}^T (\theta \mathbf{x}_1 + (1 - \theta) \mathbf{x}_2) = \theta b + (1 - \theta) b = b\]

A halfspace in $n$-dimensional space is the set of points that satisfy the inequality:

\[a_1 x_1 + a_2 x_2 + \dots + a_n x_n = \mathbf{a}^T \mathbf{x} \leq b\]

Halfspaces are also convex sets, which can be easily seen from Definition 1 or proved using Definition 2.

Norm balls

Euclidean norm balls (circles in two-dimensional space, spheres in three-dimensional space) are the set of points defined by:

\[B(\mathbf{x}_c, r) = \left\{\mathbf{x} ~\big|~ \|\mathbf{x} - \mathbf{x}_c\|_2 \leq r \right\} = \left\{\mathbf{x}_c + r\mathbf{u} ~|~ \|\mathbf{u}\|_2 \leq 1 \right\}\]

where $\mathbf{x}_c$ is the center of the ball and $r$ is the radius.

The Euclidean ball is a convex set, which can be verified by applying Definition 2. Using any norm $p \geq 1$, we still obtain convex sets.

Below is the shape of norm balls with different values of $p$:

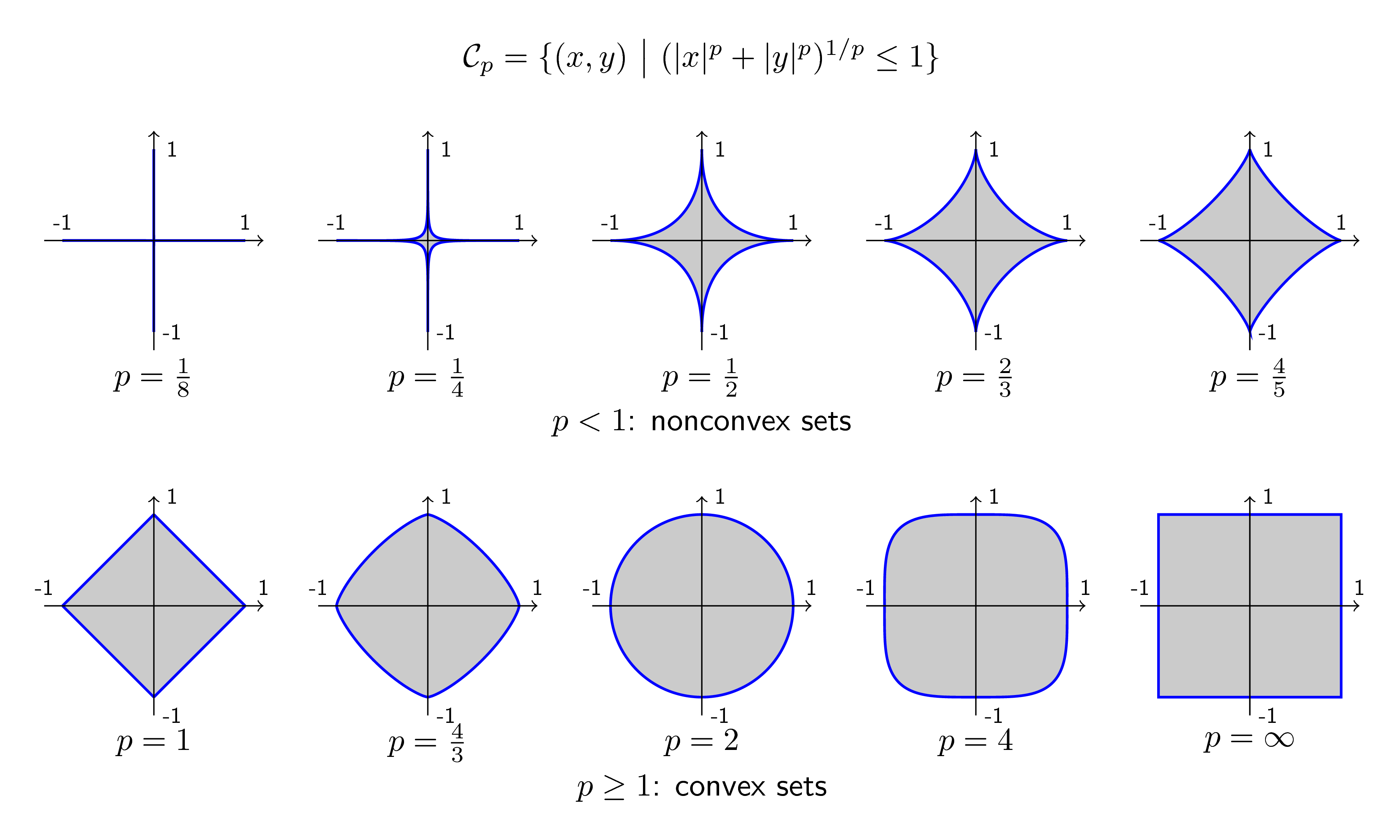
Shapes of norm balls with different $p$-norms.

For $p = 1$, the norm ball is a square. For $p = \infty$, the norm ball is a rhombus (diamond). As $p$ increases, the shape of the norm ball gradually becomes a square.

Intersection of Convex Sets

The intersection of convex sets is also a convex set. This property is intuitive from Figure 4 (left), where the intersection of two convex sets forms another convex set.

Mathematically, if $\mathbf{x}_1, \mathbf{x}_2$ lie in the intersection of convex sets, then the point $\theta \mathbf{x}_1 + (1 - \theta) \mathbf{x}_2$ will also lie in that intersection. Thus, the intersection of convex sets is itself convex.