Bagging

History of Ensemble Bagging

Bagging, short for "Bootstrap Aggregating," was introduced by Leo Breiman in the 1990s as a method to reduce the variance of decision trees. The technique involves creating multiple bootstrap samples (random samples with replacement) from the training data, training a model on each sample, and averaging their predictions. Bagging proved particularly useful for unstable learners like decision trees, which are sensitive to data fluctuations. Breiman’s Random Forests further expanded on bagging by combining bootstrap sampling with random feature selection, leading to a powerful ensemble model known for its accuracy and robustness. Bagging remains a cornerstone of ensemble methods, enhancing the stability of machine learning models.

Description Bagging, is an ensemble meta-algorithm in machine learning used to enhance the stability and accuracy of models, particularly for tasks in classification and regression. By reducing variance, bagging effectively mitigates overfitting, making it especially useful for high-variance algorithms like decision trees. Though typically used with decision trees, bagging can apply to any model, making it a versatile approach in model averaging.

Technique

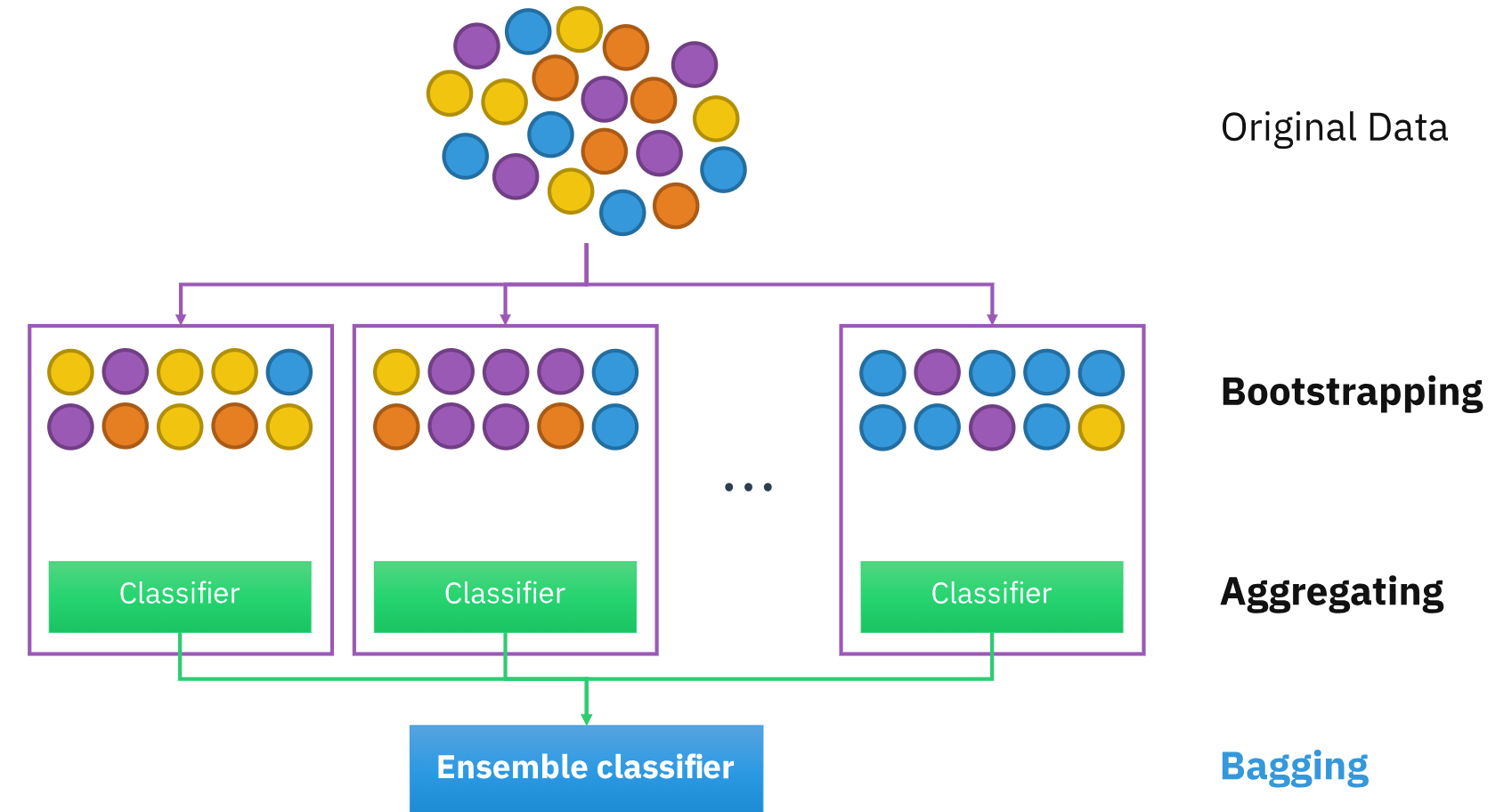
Given a standard training set $D$ of size $n$, bagging generates $m$ new training sets $D_i$, each of size $n’$, by sampling from $D$ uniformly with replacement. Sampling with replacement creates bootstrap samples, where each $D_i$ may contain repeated observations. When $n’ = n$ and $n$ is large, each bootstrap sample $D_i$ will, on average, contain around $(1 - 1/e) \approx 63.2\%$ unique examples from $D$, with the remainder being duplicates.

After creating the $m$ bootstrap samples, each sample $D_i$ is used to train a separate model $M_i$. For prediction, the bagging ensemble combines the output of each model by averaging (in regression) or majority voting (in classification), producing a final, aggregated prediction.

Datasets in Bagging

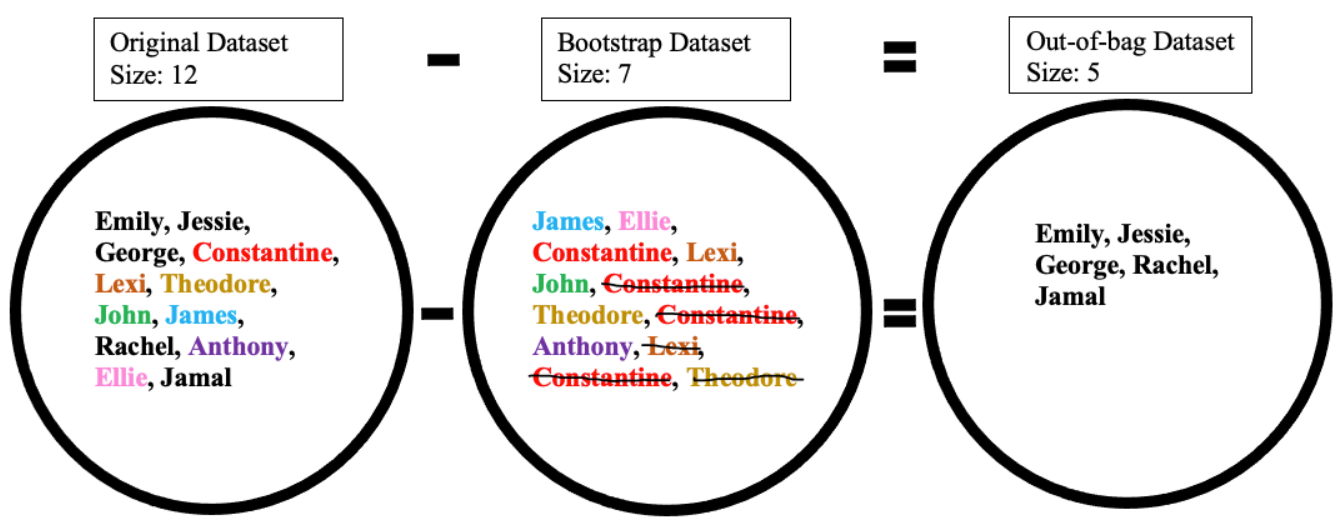
Bagging involves three main datasets:

• Original Dataset: The initial dataset, containing all samples.

• Bootstrap Dataset: Created by sampling with replacement from the original dataset, containing some duplicates, and it has the same size as the original dataset.

• Out-of-Bag (OOB) Dataset: The samples left out during bootstrapping, which can be used to assess model accuracy.

Classification Algorithm Process using Bootstrap Sampling

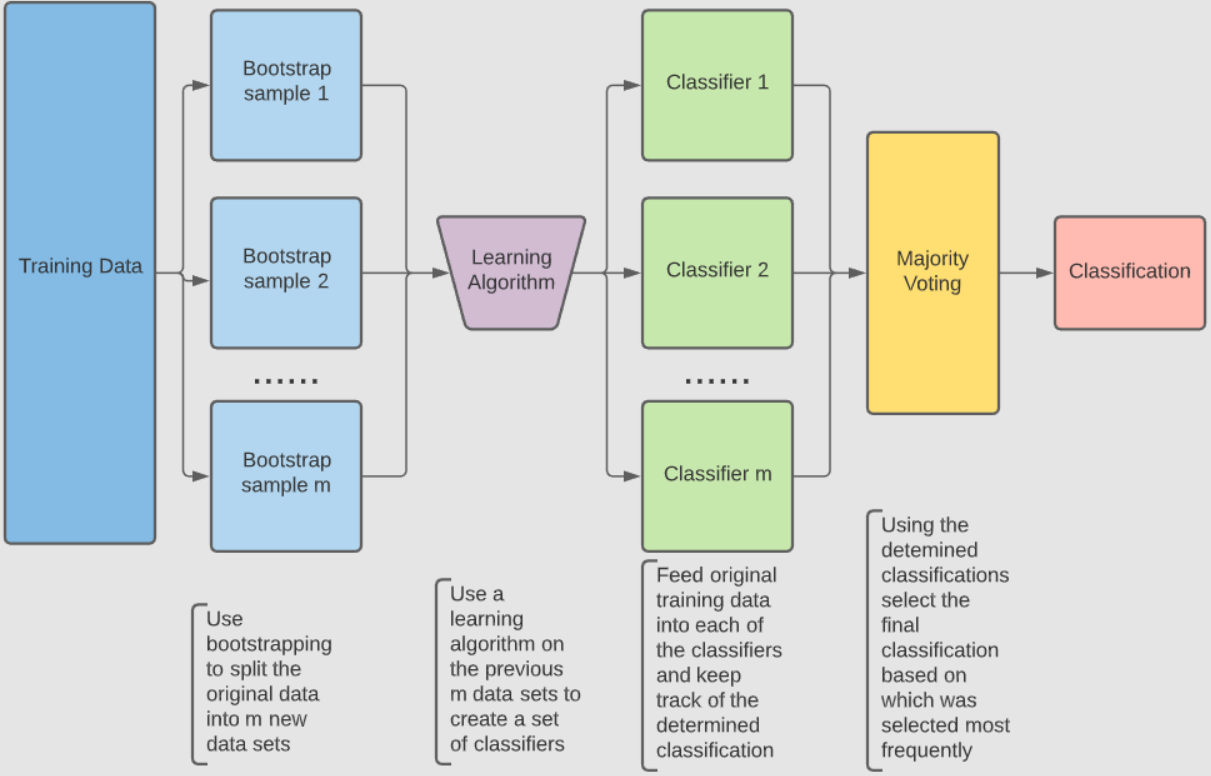
For classification tasks, we can use a bootstrap-based ensemble algorithm, which combines predictions from multiple classifiers. Given a training set $D$, an inducer $I$, and the number of bootstrap samples $m$, the following steps outline the process to generate a final classifier $C^*$:

1. Generate Bootstrap Samples: Create $m$ new training sets $D_i$ by sampling from $D$ with replacement.

2. Train Individual Classifiers: For each bootstrap sample $D_i$, train a classifier $C_i$ using inducer $I$.

3. Combine Classifiers for Final Prediction:

   • For each new input $x$, gather predictions from all classifiers $C_i(x)$.

   • For Classification: Use majority voting to determine the final predicted label \(C^*(x)\), defined as: \(C^*(x) = \arg \max_{y \in Y} \#\{i : C_i(x) = y\}\) where $Y$ is the set of possible labels, and the prediction $C^*(x)$ is the label most frequently predicted by classifiers $C_i$.

Advantages and Disadvantages of Bagging

• Advantages:

  • Reduces Variance: By averaging predictions over multiple models, bagging reduces the variance, which helps in achieving better generalization.

  • Minimizes Overfitting: Bagging is effective in reducing overfitting, particularly when the base learners are prone to high variance (e.g., decision trees).

  • Parallelization: Each model in the ensemble is trained independently on its bootstrap sample, making bagging suitable for parallel processing and thus faster on distributed systems.

  • Handles Nonlinear Relationships Well: Bagging is highly effective in capturing complex, nonlinear patterns in the data when used with nonlinear base learners.

  • Robustness to Outliers and Noise: The averaging effect in bagging can provide resilience to noise and outliers, as extreme predictions from individual models are smoothed out in the final prediction.

  • Improves Stability with Small Data Sets: With bootstrap sampling, bagging can enhance the robustness of models trained on smaller data sets by creating diverse subsets, which helps mitigate issues related to limited data.

• Disadvantages:

  • Limited Reduction in Bias: Bagging primarily reduces variance; it does not address the bias in base learners. If the base model has high bias, bagging will not significantly improve accuracy.

  • Reduced Interpretability: Since bagging combines multiple models, the ensemble’s interpretability is reduced. It is challenging to interpret the combined predictions in real-world applications.

  • Computationally Intensive: Training multiple models on bootstrapped datasets requires more computational power and memory, making bagging resource-intensive, especially with a large number of base learners.

  • May Not Always Improve Performance: If the base model is already stable with low variance, bagging may yield minimal improvements in accuracy while adding computational overhead.

  • Sensitivity to Parameter Selection: Bagging can be sensitive to hyperparameters, such as the number of bootstrap samples and the choice of base learner, which can affect its performance and require careful tuning.

  • Potential Data Redundancy: Bootstrap sampling with replacement may lead to data redundancy within individual models, as some instances may appear multiple times, which may not always add diversity.