27. Sequential Learning
Sequential Learning
Concept of Sequential Learning and Sequential Models
Sequential learning is essential for datasets where instances are ordered temporally or logically. Unlike traditional machine learning, which assumes data points are independently and identically distributed (i.i.d.), sequential learning models respect the order and dependencies between data points. Sequence models excel in tasks such as language modeling, speech recognition, and time-series prediction.
Sequential Data
Sequential data refers to datasets where points are dependent on neighboring points. Examples include:
-
Time-Series Data: Predicting future stock prices based on historical trends.
-
Text: Predicting the next word in a sentence from prior context.
-
Audio/Video Sequences: Recognizing spoken words or identifying actions in a video.
Types of Sequential Models
Sequential models are specially adapted neural networks capable of retaining memory of prior inputs. Common models include:
Recurrent Neural Networks (RNNs)
RNNs process sequences with an internal memory mechanism.
Types of RNN Architectures:
-
One-to-One: With one input and one output, this is the classic feed-forward neural network architecture. Standard input-output mapping.
-
One-to-Many: This is referred to as image captioning. We have one fixed-size image as input, and the output can be words or phrases of varying lengths.
-
Many-to-One: This is used to categorize emotions. A succession of words or even paragraphs of words is anticipated as input. The result can be a continuous-valued regression output that represents the likelihood of having a favourable attitude.
-
Many-to-Many: This paradigm is suitable for machine translation, such as that seen on Google Translate. The input could be a variable-length English sentence, and the output could be a variable-length English sentence in a different language. On a frame-by-frame basis, the last many to many models can be utilized for video classification.
Traditional RNNs, as you may know, aren’t very excellent at capturing long-range dependencies. This is primarily related to the problem of vanishing gradients. Gradients or derivatives diminish exponentially as they move down the layers while training very deep networks. The problem is referred to as the Vanishing Gradient Problem.
Long Short-Term Memory Networks (LSTMs)
LSTMs address RNNs’ long-term dependency issues with cell states and gates (input, forget, and output) that regulate information flow. They are suitable for long-sequence applications like translation.
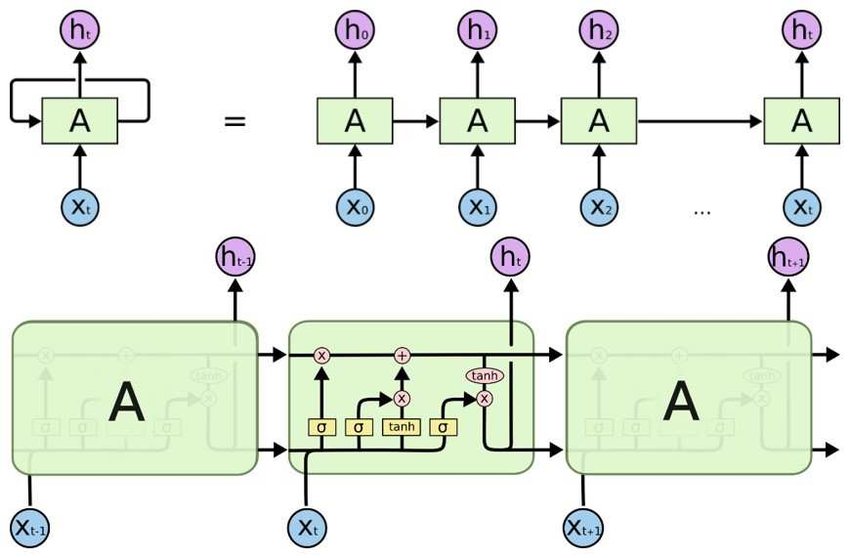
Basic Structure
At the top of the image, we observe a standard Recurrent Neural Network (RNN) structure, where each time step $t$ is represented by a cell labeled $A$. Each cell processes the input $X_t$ at that time step and passes the hidden state $h_t$ to the next time step. This creates a sequence of computations that connect each input to subsequent ones.
RNNs pass information from one time step to the next using a single hidden state, $h_t$, which retains information about the previous inputs in the sequence. However, this simple structure struggles with retaining long-term dependencies due to issues like the vanishing gradient problem.
Unfolding in Time
The RNN structure is "unfolded" across time, as shown by multiple cells (each labeled $A$) connected in sequence from $X_0$ to $X_t$. This representation illustrates that the network reuses the same cell architecture for each time step.
In both RNN and LSTM architectures, unfolding the network in time shows how the model processes sequences step-by-step. However, unlike basic RNNs, LSTMs have additional mechanisms to better retain long-term dependencies.
LSTM Internal Structure
The lower part of the image focuses on the LSTM cell’s internal workings. Unlike the simple RNN cell, an LSTM cell has a more complex structure with multiple gates: the forget gate, input gate, and output gate. These gates control the flow of information through the cell and allow it to retain important information for longer periods.
The LSTM cell introduces a cell state (often represented as $C_t$), which runs horizontally across time steps. This cell state provides a way to retain information over long sequences, solving the vanishing gradient problem inherent in RNNs.
Gates in LSTM
Each gate in the LSTM cell performs specific functions:
-
Forget Gate: In the LSTM cell shown in the lower part of the image, the forget gate is represented by the symbol sigmoid ($\sigma$) connected to a multiplication operation. This gate controls which parts of the cell state are discarded by scaling them down to zero or retaining them. This operation helps the cell "forget" unnecessary information from the previous time step.
-
Input Gate: The input gate is represented by another sigmoid symbol followed by a multiplication (×) operation and a tanh operation. This part decides which new information will be added to the cell state. The output from the input gate (after the sigmoid and tanh transformations) is combined with the cell state, adding new relevant information.
-
Output Gate: The output gate is shown by the third sigmoid ($\sigma$) and a subsequent multiplication with the cell state after a tanh transformation. This gate determines the final hidden state $h_t$ that will be passed on to the next time step. This hidden state is essentially the cell’s output and is influenced by both the current input and the long-term information retained in the cell state.
These gates are implemented using sigmoid ($\sigma$) and tanh activations, allowing the network to learn which information to retain, update, or forget as it processes each time step.
Advantages of LSTM over RNN
-
Memory Retention: Due to the additional cell state and gating mechanisms, LSTMs can retain important information over long time sequences, making them effective for tasks that require long-term dependencies.
-
Mitigation of Vanishing Gradients: By carefully regulating information flow, LSTMs address the vanishing gradient issue that limits the performance of standard RNNs on long sequences.
Autoencoders
One of the most active study areas in Natural Language Processing is machine translation (MT) (NLP). The goal is to create a computer program that can quickly and accurately translate a text from one language (source) into another language (target) (the target) The encoder-decoder model is the fundamental architecture utilized for MT using the neural network model:
-
The encoder sub-section summarizes the data in the source sentence.
-
Based on the encoding, the decoder component generates the target-language output in a step-by-step manner.
The performance of the encoder-decoder network diminishes significantly as the length of the input sentence increases, which is a limitation of these approaches. The fundamental disadvantage of the earlier methods is that the encoded vector must capture the full phrase (sentence), which means that much critical information may be missed.
Furthermore, the data must “flow” through a number of RNN steps, which is challenging for large sentences. Bahdanau presented an attention layer that consists of attention mechanisms that give greater weight to some of the input words than others while translating the sentence and this gave further boost in machine translation applications.
Sequence-to-Sequence (Seq2Seq)
Seq2Seq models handle variable-length input and output sequences, making them essential for tasks like translation, summarization, and dialogue generation. They consist of an encoder to process the input and a decoder to generate the output.
Applications of Sequential Models
-
Natural Language Processing: Sentiment analysis, translation, text generation.
-
Speech and Audio Processing: Recognition and synthesis.
-
Predictive Analysis: Stock and weather forecasting.
-
Healthcare: Patient history analysis for diagnosis.
-
Genomics: DNA sequence classification and prediction.


