Noise and Outliers in Data Analysis

Definitions

Noise refers to any unwanted anomaly in the data that complicates the learning process and may make achieving zero error infeasible with a simple hypothesis class. Noise can arise in various forms:

• Input Noise: Imprecision in recording input attributes can cause shifts in data points within the input space.

• Label Noise (Teacher Noise): Errors in labeling may incorrectly categorize positive instances as negative, or vice versa.

• Latent or Hidden Attributes: Additional unobserved attributes may affect the label of an instance. These neglected attributes are modeled as a random component and considered part of the noise.

Noise introduces variability that can obscure true patterns in data, making the learning process more challenging.

Outliers, on the other hand, are data points that significantly deviate from other observations. They may arise from data entry errors, experimental inaccuracies, or rare events, but they can also contain meaningful information about the underlying system. Outliers are often referred to as abnormalities, discordants, deviants, or anomalies.

Outliers are broader in scope compared to noise, as they include not only errors but also discordant data that may arise naturally from variations in the population or process. They are particularly valuable in fields such as fraud detection, intrusion detection, weather forecasting, and medical diagnosis, where identifying anomalies can lead to significant insights.

In the medical domain, common sources of outliers include equipment malfunctions, human errors, and patient-specific anomalies. For example, an abnormal blood test result could be due to pathology, medication intake, recent physical activity, or even improper sample handling. Evaluating whether an outlier represents an important finding or an error is crucial before any corrective action is taken.

Handling Noise and Outliers

Handling Noise

Noise can be managed through various data preprocessing techniques to improve model performance:

• Data Cleaning: Detecting and removing incorrect or inconsistent data, such as correcting input errors or discarding mislabeled instances.

• Smoothing Techniques: Techniques like moving averages or Gaussian filters can reduce the impact of noise in continuous data by smoothing variations.

• Dimensionality Reduction: Methods like Principal Component Analysis (PCA) can help reduce noise by focusing on the most informative components.

• Robust Models: Choosing models that are less sensitive to noise, such as robust regression or decision trees, which inherently ignore small fluctuations.

Handling Outliers

Outliers require careful handling to avoid removing valuable information or introducing bias:

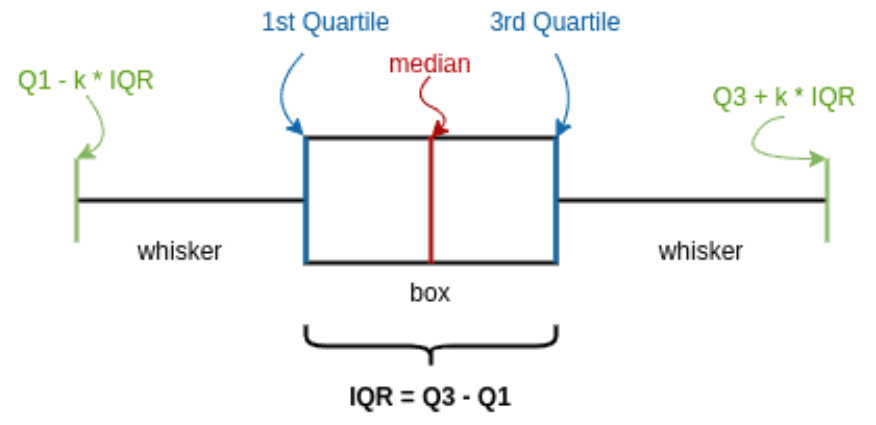
• Statistical Methods: Techniques such as Z-score, Interquartile Range (IQR), and modified Z-score help detect outliers based on statistical thresholds.

• Clustering-Based Methods: In complex datasets, clustering algorithms (e.g., DBSCAN) can identify outliers as points that do not belong to any cluster.

• Model-Specific Detection: Regression-based models are suitable for linearly correlated data, while neural networks or ensemble models may better handle nonlinear distributions.

• Domain Knowledge: Incorporating domain-specific insights, especially in fields like medicine, can help decide whether to retain, modify, or remove an outlier.

Comment: The choice of method depends on the data type, size, distribution, and the need for interpretability, especially in high-stakes fields like healthcare.

Comparison of Noise and Outliers

Attribute	Noise	Outlier
Definition	Random or irrelevant data that obscures true patterns.	Data points that significantly deviate from other observations, often called abnormalities or anomalies.
Source	Often due to measurement errors, environmental factors, or sensor inaccuracies.	Can result from data entry errors, rare events, or natural variations within the population.
Impact on Model	Generally reduces model accuracy by introducing random variability.	May affect model accuracy but can also represent meaningful insights or anomalies.
Detection Methods	Identified through signal processing, filtering, or data cleaning techniques.	Detected through statistical methods like Z-score, IQR, clustering, or regression analysis.
Treatment	Typically removed or smoothed to enhance model clarity.	Can be removed, retained, or corrected depending on their cause and potential significance.